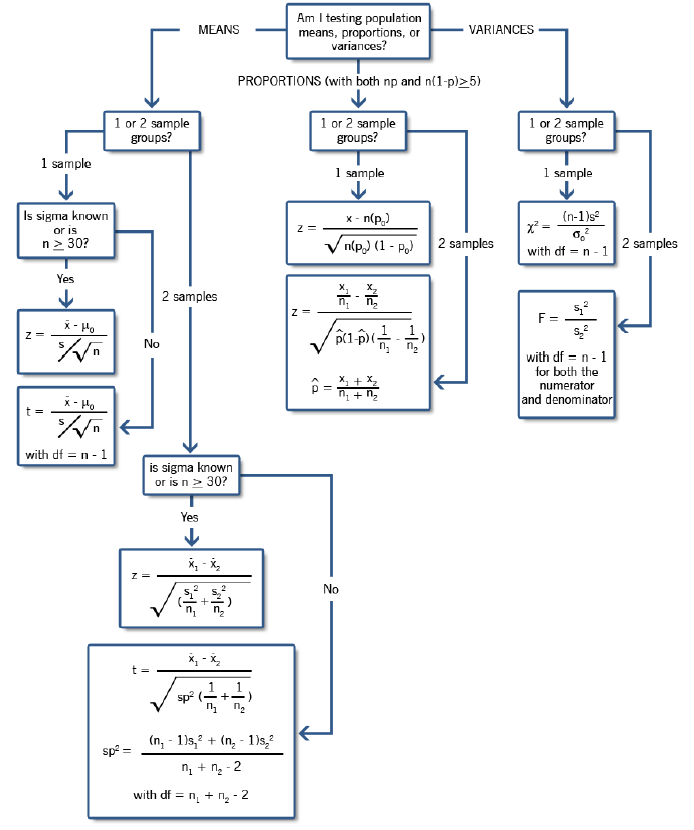
There are four possible outcomes when making hypothesis test decisions from sample data. Two of these outcomes are correct in that the sample accurately represents the population and leads to a correct conclusion, and two are incorrect, as shown in the following figure:
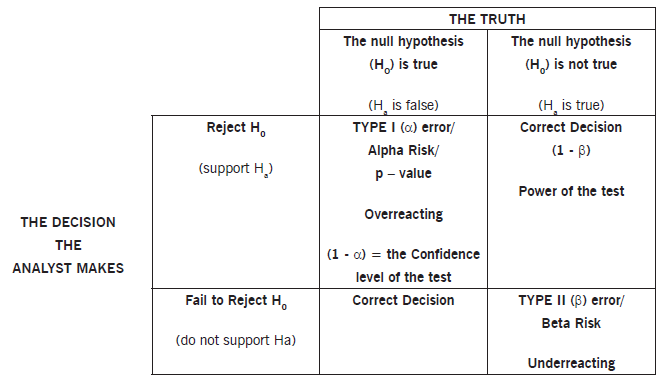
TYPE I ERROR (or α Risk or Producer’s Risk)
In hypothesis testing terms, α risk is the risk of rejecting the null hypothesis when it is really true and therefore should not be rejected. In other words, the alternative hypothesis is supported when there is inadequate statistical evidence for doing so (too much risk). This can be thought of as overreacting to data results that might be due just to chance alone.
The most commonly used level of β risk is .05, or 5%. This level of β risk means that there is a 5% chance that the sample results are due to chance alone, so there is a 5% chance that rejecting the null hypothesis (supporting the alternative hypothesis) will be an incorrect decision.
TYPE II ERROR (or β Risk or Consumer’s Risk)
In hypothesis testing terms, β risk is the risk of failing to reject the null hypothesis when it is really false and therefore should be rejected. In other words, the alternative hypothesis is not supported even though there is adequate statistical evidence to show that supporting it meets the acceptable levels of risk. This can be thought of as underreacting to data results that are probably real and not due just to chance alone.
The most commonly used level of β risk is .10, or 10%. This level of β risk means that there is a 10% chance that the sample results are not due to chance alone, so there is a 10% chance that failing to reject the null hypothesis (failing to support the alternative hypothesis) will be an incorrect decision.